Coupled Springs

Coupled differential equations are ubiquitous.You can find them anywhere from a creaking chair to human interactions. They are important not only from a physics point of view about solving coupled springs or coupled LCR circuits or in chemistry for knowing how reaction rates behave or in biology for knowing the population dynamics or in economics for knowing how markets behave but something bigger than that. Coupled equations are the underlying thread which connects every activity to every other activity.And it is not at all a bad assumption to allow for other systems interacting with your system or vice versa. It is not possible,except in very clean physics experiments(and too with difficulty), to seperate the concerned quantity with other related quantities,many a times,it might be that we are interested in the interaction itself or sometimes wanting to seperate it. Differential equations govern the dyanmics of any system and since nothing is independent on this universe,everything is linked to everything,we need to consider and perhaps only consider coupled differential equations to predict future of the system (it could be the world,who knows).
So to give a flavour of it.I will start with a simple example of two springs linked to each other.
Some notes
1. You can use any mathematical software to get these equations automatically solved (like Mathematica,Matlab).Also online www.wolframalpha.com can solve equations for you.
You need not visualise these equations as connected springs,it could be anything such that the dyanmics of our desired qunatity x1(position of spring from equilbiria, no of rabbits, conc. of chemical etc) id affected by certain other connected qunatity(another spring, no of mothers,chemical's quencher etc).
Consider the following coupled differential equation.
  d^2 x1/ dt^2 = - x1 + e x2
 d^2 x2/dt^2 = e x1 - x2
So here if e was zero,we would say that the system of equations are independent and their solutions are obtained every easily.
 d^2 x1/dt^2 = -x1
 d^2 x2/dt^2=-x2
An ansatz like x1= A exp(i t) +  B exp(-i t) and x2=C exp(i t) + Dexp(-i t) works.
How we came about this guess is also an interesting story (which includes the power series of solving differential equation) which i hope i will cover in some other post.
But the picture till now is: given independent differential equations,we can solve it and find out the dyanmics of the system quite easily.

whose solution when plotted with respect to time shows sinusoidal behaviour as expected due to presence of cos and sin term in the solution (Euler's formula).
Now when we introduce the dependence of our independent springs on each other (probably by connecting them),then we can manipulate the strentgh of connection by changing the magnitude of e.
First of all,how to solve such a kind of equation.
Simple answer is,give it to some mathematical software like Matlab who will solve it for you.

If you dont want to read further and know the answer.
 For e=0.001

The first image is for the first equation,and second image for second equation.
For e= 0.1

First image for first equation
second image for second equation
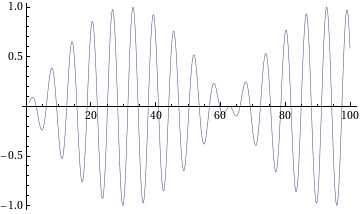
e=1

It would be better if we plotted them together

Notice how the systems have coupled themselves together such that behaviour of one is enough to predict the behaviour of other one.
The extent of coupling allows us to know the other systems better and better by knowing the dynamics of just one system (provided we also know the type of coupling ,linear,quadratic,exponential).

Otherwise,
Note the any linear operation on vectors which live in a vector space (defined over the complex field) is just transforming a vector from one form to another in the same vector space.say you had the vector (3,2) and you mutiply it by a matrix ((0,1),(1,0)) which will flip the x and y coordinates of the vector and hence take it to another place in the same space.Since every abstract vector space can be operated on by using a basis (a basis makes any abstract vector space look like C^n or R^n depending on your field),any linear transformation corresponds to mutlitplyign the vector by a matrix which transforms the vector.
Matrix multiplication is a simple thing.Ain't it?
But realise that the operation d^2/dt^2 is also linear on vector space V,such that it L(x+y) = L(x) + L(y) and L(c x) = cL(x),here L = d^2/dt^2.
Now that we know this double differentiation operation is linear,we can diagonalize it which means seperate the vector space into smaller subspaces such that any vector can be uniquely decomposed and each component of the vector is contained in these invariant subspaces.
But there's a theorem that whenever a matrix/linear transformation has distinct eigenvalues,it is diagonalizale. So lets check if our matrix of linear transformation is diagonalizable. (just check if its determinant is non zero).

Yet to be completed.
i will go through
1. diagonalizing the matrix of linear transformation and decoupling the given system of equations
2. How does the dyanmics depend on intital points (so called phase factor)
3. Extent of coupling.
4. Non linearity.